In this article, we will also solve several practical problems using bitwise operations:
- Get the last bit from an integer
- Get the bit at a certain index from an integer
- Change the bit at a certain index in an integer
- Extract the bit before the last from an integer
If you are not familiar with bits and storing data on the computer you can read our previous articles about them here:
Bitwise Operations
First, let’s start with learning about the bitwise operations in programming. They work with the binary representations of the numbers, applying bit-by-bit calculations. For example, if we have two 8-bit numbers, we can apply a bitwise operation, which takes as input the first 8 bits and the second 8 bits and produces as a result new 8 bits.
A simple bitwise operator over a single argument is the “tilde” operator – the bitwise logical NOT (also called negation). The operator “tilde” turns all zeroes to ones and all ones to zeroes, like the “exclamation mark” operator for the Boolean expressions, but it works bit by bit. For example, if we have the binary number “1 0 0″, its negation “tilde 1 0 0” is “0 1 1“.
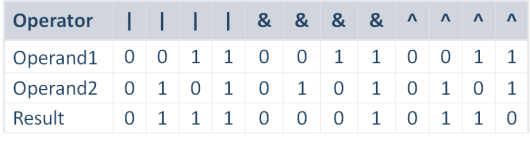
The table above illustrates the work of the bitwise OR, AND, and XOR operators.
- The bitwise OR operator (denoted by the vertical bar in most programming languages) returns 1, if one of its input bits is 1, otherwise returns 0.
- The bitwise AND operator (denoted by the ampersand in most programming languages) returns 1, if both of its input bits are 1, otherwise returns 0.
- The bitwise exclusive OR (XOR) operator (denoted by the ampersand in most programming languages) returns 1 if one of its arguments is 1, but not both at the same time, otherwise returns 0.
Bit Shifts
Bit shifts are bitwise operations, where bits inside a number are moved (or shifted) to the left or the right. During the shifting operation, the bits that fall at invalid positions are lost, and the bits which come from missing positions are replaced by 0.
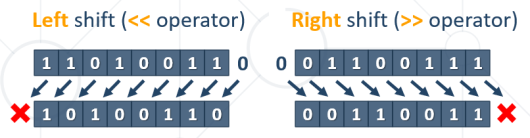
Bit shifting can be applied for 8-bit, 16-bit, 32-bit, and 64-bit numbers, as well as for numbers of other sizes in bits. The bit size of the number being shifted defines the valid bit positions and where the bits get lost. Bits can be shifted by more than 1 position. For example, 5 shifted left twice is 20 and 5 shifted right twice is 1.
Why We Need Bitwise Operations?
Processing bits is important for many fields of computer science, information technologies, and software systems, like networking protocols, data storage, and file systems, binary file formats, memory management, data compression, data encryption, video streaming, Internet of things (IoT) systems, low-level programming, computer graphics, and many others.
Data compression algorithms replace bit or byte sequences with shorter bit sequences. For example, the “DEFLATE” algorithm, used to compress data in the ZIP files, finds the most often sequences and replaces them with shorter sequences, while it preserves a dictionary between the original bit sequences and their shorter compressed form. This is done using heavy bit-level processing with bitwise operations.
Many binary file formats use bits to save space. For example, PNG images (the Portable Network Graphics image format) use 3 bits to specify the color format used (8-bit color, 24-bit color, 32-bit color with transparency). These 3 bits are located at a certain offset in the PNG image header bytes, so reading and writing the value encoded in these 3 bits require bitwise operations.
To sum it up, bitwise operators work with the binary representations of the numbers, applying bit-by-bit calculations. Bit shifts are bitwise operations, where bits inside a number are shifted to the left or the right. These concepts are an important aspect of many fields of computer science.
Lesson Topics
Bitwise Operations
Bitwise Operators – Examples
Bit Shifts
Bitwise Operations Problems
Why We Need Bitwise Operations?
Bit Before the Last – Problems



