In this lesson, we will talk about numeral systems, which are widely used in computer programming. By the end of it, you will know how to use the binary, decimal, and hexadecimal numeral systems, their characteristics, and how to convert integers from one numeral system to another.
Numeral systems represent numbers in written form using sequences of digits. For example: the digit “4“, followed by the digit “2” in the traditional decimal system used by humans, represents the number “42“.
Many systems can be used to represent numbers, like the Hindu–Arabic numerals, the Roman numerals, and the Hebrew numerals. In computer science, specific numeral systems are of big importance: the positional numeral systems. In the positional numeral systems, the value of each digit depends on its position. In the integer numbers, the digits on the left have a bigger weight than the digits, staying on the right.
Positional numeral systems use the so-called base (a number like 2, 10, or 16) that specifies how many digits are used to represent a number. For example, the decimal system uses 10 digits: 1, 2, 3, 4, 5, 6, 7, 8, 9, and 0. The binary system uses only two digits: 1 and 0. The hexadecimal system uses 16 digits: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, and F.
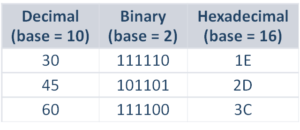
On the image, you can see the decimal, binary and hexadecimal representations of the numbers 30, 45, and 60.
Decimal numbers use a positional numeral system of base 10. Decimal numbers are the traditional numbers used by humans in their everyday life.
Decimal numbers are represented by the following 10 digits: 0, 1, 2, 3, 4, 5, 6, 7, 8, and 9.
Each position in a decimal number corresponds to a certain power of 10. The rightmost position is multiplied by 1 (which is 10 raised to the power of 0), the next position on the left is multiplied by 10 (which is 10 raised to the power of 1), the next position on the left is multiplied by 100 (which is 10 raised to the power of 2), and so on.
Four hundred and one is equal to:
- 4 multiplied to 10 to the power of 2 + 0 multiplied to 10 to the power of 1 + 1 multiplied to 10 to the power of 0
- which is equal to 4 multiplied by 100 + 0 multiplied by 10 + 1 multiplied by 1
- which is equal to 400 + 0 + 1
- which is equal to 401

We can think of decimal numbers as polynomials of their digits in the following form:
![]()
The binary numeral systemis fundamental for computer systems. It uses base 2 and only two digits: 1 and 0. Binary numbers (numbers of base 2) are sequences of zeroes and ones. For example: 5 (in decimal) is equal to 1 0 1 in binary. We denote binary numbers with a small suffix “b” at the end.
Hexadecimal numbers (also known as hex numbers) are widely used in computer science. Hex numbers use base 16 and are represented by a sequence of hex digits. The hex digits are the following literals: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, and F. Note that after 9 the next digit is A, which has a decimal value of 10. The next hex digits after A are B, C, D, E, and F and they have decimal values of 11, 12, 13, 14, and 15. These decimal values are used when we convert a hex number to a decimal value.
That is the main idea about numeral systems. They are used by humans, and computers, to write numbers using digits. It is something that you shouldn’t take lightly, and be careful!
Lesson Topics
Numeral Systems
Decimal Numbers
Binary Numbers
Binary and Decimal Conversion
Hexadecimal Numbers
Hex to Decimal Conversion
Hex to Binary Conversion



